Интерферометры Фабри-Перо
Сканирующие интерферометры Фабри- Перо
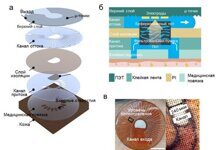
Сканирующие интерферометры Фабри-Перо состоят из резонатора, образованного парой идентичных зеркал и разнесенных друг от друга на величину радиуса кривизны (см. рис. 1), который для обоих зеркал одинаков. Эта конфигурация также называется конфокальным резонатором и имеет свойство селекции мод. Вырождение мод с одинаковыми продольными и разными поперечными индексами происходит вследствие совпадения их резонансных частот.

Рисунок 1. Схема резонатора, состоящего из двух зеркал, разнесенных на некоторое расстояние
Вырождение мод значительно упрощает юстировку прибора, поскольку устраняется необходимость согласования индексов мод внутри резонатора. Конфокальные резонаторы имеют ряд преимуществ перед плоскопараллельными интерферометрами, поскольку невосприимчивы к угловому выравниванию.
Резонаторы Фабри-Перо сохраняют добротность и оптический фактор даже при повышении разрешающей способности. Плоско-параллельные резонаторы не обладают этим свойством, повышение разрешения неизбежно сопровождается снижением интенсивности и оптического фактора (оптический фактор определяется как излучение внутри телесного угла Ω к участку апертуры площадью А).
Внутренняя вогнутая поверхность зеркал покрывается отражательным слоем, внешняя полностью матовая. Кривизна внешней поверхности соответствует кривизне внутренней, создавая так называемый линзовый эффект. В конфокальной системе зеркала разнесены на величину радиуса кривизны r (см. рис. 1).
Чтобы проследить принцип работы резонатора, проследим ход луча в резонаторе. Излучение попадает в резонатор под некоторым углом на высоте Н (отсчитывается от одной из стенок резонаторной полости). Доля прошедшего излучения проходит по траекториям 1, 2, 3 и 4, а затем снова попадает на траекторию 1. Цикл повторяется. Пунктирные линии, внешние по отношению к полости на рисунке 2, представляют часть излучения, отраженного при входе в резонатор, тогда расстояние, пройденное излучением туда и обратно равно mλ, где m - целое число, а λ - длина волны входного излучения. Приблизительная длина оптического пути L одного цикла в резонаторе может быть выражена как:
 (1)
(1)

Рисунок 2. Путь внеосевого луча, проходящего в резонаторе
Резонанс и область свободной дисперсии
Для достижения максимального резонанса в интерферометре Фабри-Перо полный фазовый сдвиг за один полный проход излучения в резонаторе должен быть кратным 2π. В плоско-параллельной конфигурации резонатора Фабри-Перо, где расстояние туда и обратно внутри полости равно 2r, условие максимума резонанса выполняется, когда частота равна mc/2r (m - любое целое число, c - скорость света в воздухе, а r - расстояние между зеркалами. Следовательно, расстояние, или область свободной дисперсии между двумя пиками пропускания составляет c/2r.
В конфокальном резонаторе Фабри-Перо нужно учитывать, что моды резонатора – Гауссовы. Принимая во внимание фазовый сдвиг Гауссовой моды в конфокальном резонаторе, можно показать, что резонансные частоты поперечных мод либо перекрываются, либо оказываются точно посередине между амплитудами продольных мод. Поэтому область свободной дисперсии конфокального резонатора составляет c/4nd.
Точный расчет круговой траектории
Поскольку фактическая длина оптического пути в конфокальном интерферометре Фабри-Перо зависит от высоты вхождения пучка Н, на практике важно учитывать входные параметры системы, апертуру и диаметр пучка. Все это напрямую влияет на условия резонанса.
Чтобы связать уравнениями разрешающую способность интерферометра и высоту Н, нужно принять во внимание сферические аберрации. В приближении 0 < H << r выражение длины оптического пути имеет вид:
 (2)
(2)
Можно видеть, что с ростом диаметра входного пучка, второй компонент выражения (2) стремительно возрастает.
Добротность и разрешающая способность конфокального резонатора
Добротность резонатора – это способность интерферометра разрешать близко расположенные спектральные линии. Минимальное приращение частоты интерферометра, при котором спектральные линии можно рассмотреть отдельно, рассчитывается по критерию Рэлея: для разрешения двух близко расположенных линий равной интенсивности и симметричного контура необходимо, чтобы центральный максимум одной линии совпадал с первым минимумом другой (рис. 3).

Рисунок 3. Изображение двух спектральных линий Гауссового профиля, разрешенных в интерферометре:расстояние между резонансными пиками равно полной ширине на уровне половинной высоты (FWHM Δ)
Общая добротность интерферометра определяется отношением величины области свободной дисперсии FSR к полной ширине на полувысоте FWHM Δ резонансного
пика. Как видно из рис. 3, две линии, расстояние между резонансными пиками которых Δ, удовлетворяют критерию Рэлея. Так, разрешение системы равно Δ.
Полная добротность определяется выражением:
 (3)
(3)
В процессе производства интерферометров поддерживается максимум полной добротности, чтобы можно было более точно отрегулировать длину резонаторной полости в конфокальной конфигурации. Также длину резонаторной полости можно настраивать по длине волны, однако этот способ менее точен.
Область свободной дисперсии и полная ширина на полувысоте показаны, соответственно, на рисунках 4 и 5. Показатель добротности 294 измерен с помощью лазера с распределенной обратной связью. Ширина спектральной линии не может считаться бесконечно малой по сравнению с разрешением резонатора, а потому истинное значение добротности составляет около 320, при условии ширины линии лазера 2 МГц.

Рисунок 4. Вид области свободной дисперсии интерферометра: получен с помощью лазера c распределенной обратной связью серии PRO8000 Thorlabs, система из интерферометра SA200-12B Thorlabs с областью свободной дисперсии 1.5 ГГц применяется для калибровки временной оси осциллографа, зная область свободной дисперсии интерферометра, коэффициент калибровки определяется подбором соответствия 1.5 ГГц - 20 мс между двумя пиками

Рисунок 5. Реальный сигнал лазера в масштабе: график является результатом свертки ширины спектральной линии лазера и добротности резонатора, с помощью откалиброванной временной шкалы осциллографа (рис.4) определяется полуширина на полувысоте сигнала для интерферометра: 0.068 мс · 75 МГц/мс = 5.1 МГц, эта частота обеспечит нижний предел добротности, равный 294
На добротность влияют многие факторы: коэффициент отражения зеркал FR, качество зеркальной поверхности Fq, а также качество излучения (главным образом диаметр пучка) и выравнивание зеркал. Для обратных величин получаем:
 (4)
(4)
где для зеркал, коэффициент отражения которых близок к 1, эффективная добротность отражения зеркал рассчитывается как:
 (5)
(5)
R – коэффициент отражения зеркала.
Хотя определение добротности отражения условно, уравнение (5) все же принимается как эффективная добротность отражения, когда другие факторы влияния пренебрежимо малы. В таких случаях основной вклад вносит источник излучения.
По формуле (5) проектируются отражающие покрытия в интерферометрах. Наименьшее значение FR должно быть более чем в 1.5 раза выше добротности отражения во всем рабочем диапазоне длин волн для конкретной модели. Это вносит поправку в первый член уравнения (4).
Второе слагаемое в формуле (4) содержит Fq – неровности зеркальной поверхности, которые вызывают симметричное уширение спектральной линии. Результатом этих неровностей является случайная зависящая от положения разница в длине пути, которая и расширяет форму линии. При производственном процессе изготовления зеркал резонатора гарантируется, что вклад от Fq пренебрежимо мал по сравнению с указанной полной добротностью.
Последний член в формуле (4) Fi – добротность освещения. Разрешение уменьшается при увеличении диаметра пучка или при смещении входного пучка. Когда добротность ограничена параметром Fi, форма линии будет выглядеть асимметричной. Асимметрия обусловлена разницей в длине пути между осевыми и внеосевыми пучками, что приводит к расхождению расстояний между зеркалами. В соответствии с условием максимального резонанса, примерное уменьшение длины пути пучка на расстоянии H от оптической оси резонатора задается вторым слагаемым в формуле (2).
Чтобы количественно оценить влияние длины пути на Fi, рассмотрим идеальный монохроматический входной пучок (дельта-функцию по длине волны с единичной амплитудой). Излучение попадает в резонатор Фабри-Перо вдоль оптической оси, пучок имеет радиус a.
Свет, поступающий в интерферометр в точке H = + e, где е бесконечно мал, но не равен нулю, будет лишь незначительно искажать начальный спектр.
Свет, попадающий в резонатор в точке H = + a вызовет значительный сдвиг в передаваемом выходном спектре, поскольку оптическая длина пути резонатора будет меньше на расстояние ~ a4/4r3.
Предполагая, что входной пучок имеет равномерное распределение интенсивности, передаваемый спектр будет иметь однородную интенсивность и уширение из-за изменяющейся длины оптического пути. В результате входная дельта-функция длины волны будет давать выходной пик с Δ = H4/4r3.
Предполагая, что только параметр Fi вносит значительный вклад в общую добротность, с помощью уравнения (3) можно рассчитать Fi для «идеального» входного пучка. Подставляя λ/4 вместо FSR и H4/4r3 вместо Δ получаем:
 (6)
(6)
Подстановка четверти длины волны вместо FSR оправдана, учитывая, что полость расширяется на эту величину, чтобы произошел переход от одной продольной моды к следующей. Для входного луча с реальным спектральным распределением эффект от сдвига будет представлять собой сплошную серию смещенных линий. Следует отметить, что смещение всегда происходит в одном направлении, что приводит к расширению или асимметрии.
Итак, используя уравнение полной добротности, содержащее вклады FR и Fi, можно найти:
 (7)
(7)
Заменой Fi и FR получаем:
 (8)
(8)
Уравнение (8) используется для оценки (хотя и несколько завышенной) влияния диаметра пучка на общую добротность интерферометра Фабри-Перо. Завышение происходит, поскольку соотношение теоретических предположений с практическими данными неточно: во-первых, в теории диаметр пучка совпадает с диаметром зеркала, на практике же диаметр пучка обычно значительно меньше диаметра зеркала (это также помогает уменьшить сферическую аберрацию). Другое теоретическое предположение состоит в том, что пучок пережимается до бесконечно малого фокального пятна, но в реальности даже для монохроматического света минимальный размер пятна фокусировки ограничен дифракцией, а в случае многомодовых источников размер пятна сохраняется довольно большим и в фокусе.
Рисунок 6 представляет график уравнения (8) для двух конструкций резонатора (r = 50 мм и r = 7.5 мм). Графики были построены в предположении, что добротность отражения равна 300 - наиболее типичное значение для зеркал, используемых в интерферометрах Thorlabs.

Рисунок 6. Зависимость Ft(H), найденная для двух интерферометров Фабри-Перо Thorlabs: зеленая кривая соответствует резонатору 7.5 мм, синяя кривая – резонатору 50 мм
Спектральная разрешающая способность и оптический фактор
Спектральная разрешающая способность интерферометра – это количественная мера разрешающей способности интерферометра, удовлетворяющая расширенному критерию Рэлея. Спектральная разрешающая способность SR определяется формулой:
 (9)
(9)
В уравнении (9) v – частота и λ – длина волны. Можно показать, как по этой формуле рассчитывается разрешающая способность конфокального интерферометра Фабри-Перо:
 (10)
(10)
В уравнении (10) F - добротность интерферометра, r - радиус кривизны зеркал, а λ - длина волны. Однако для достижения максимального разрешения интерферометра непосредственно в режиме сканирования, апертура детектора должна быть бесконечно мала, когда апертура открывается достаточно широко, спектральная разрешающая способность начинает уменьшаться.
Спектральная разрешающая способность должна быть сбалансирована с оптическим фактором интерферометра. Оптический фактор интерферометра U является мерой, характеризующей насколько «расширен» пучок в оптической системе по размерам и направлениям.
Когда источником света является лазерный пучок, оптический фактор определяет меру допуска центрировки между интерферометром и лазерным пучком.
Математически оптический фактор описывается как произведение максимально допустимого расхождения телесного угла Ω и максимально допустимой площади апертуры A. Для конфокальной системы оптический фактор выражается как:
 (11)
(11)
В уравнении (11) F - добротность интерферометра, λ - длина волны, а d - расстояние между зеркалами. Для правильного использования интерферометра спектральная разрешающая способность и геометрический фактор должны быть откалиброваны таким образом, чтобы достаточное количество света попадало в систему без значительного снижения разрешения интерферометра.
На практике основной компромисс для получения этого баланса заключается в увеличении апертуры зеркала до такой степени, пока спектральная разрешающая способность не уменьшится до 70% (0.7SR). При этом условии «идеальный» оптический фактор имеет вид π2λr/F , где r - радиус зеркала.
© Thorlabs Inc.
Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Thorlabs на территории РФ
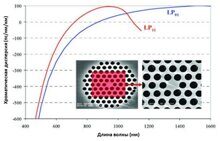
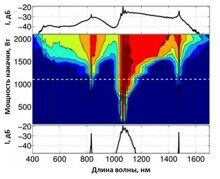
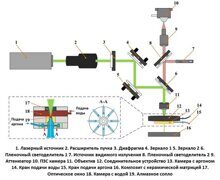
В статье описан метод генерации суперконтинуума, расширенного в видимый диапазон. За счет четырехволнового смешения накачка 1064 нм создает антистоксовы и стоксовы компоненты на 831 нм и 1478 нм. Фазовый синхронизм обеспечивается благодаря микроструктурированному мультимодальному волокну особой конструкции.
контакты
г. Санкт-Петербург, улица Савушкина 83, корп. 3