Как можно измерить силу эффекта Фарадея материала?
Поскольку эффект Фарадея вызывает вращение плоскости поляризации света при его распространении через материал в присутствии магнитного поля, один из подходов к определению силы эффекта в материале состоит в том, чтобы ввести линейно поляризованный свет, приложить к материалу сильное магнитное поле и понаблюдать за индуцированным изменением ориентации состояния выходной поляризации. Нет необходимости напрямую измерять состояние выходной поляризации, чтобы определить изменение его ориентации. Вместо этого выходной свет можно анализировать путем измерения оптической мощности, передаваемой через вращающийся линейный поляризатор. Измеренная мощность колеблется с фазой, зависящей от ориентации состояния линейной поляризации, падающей на вращающийся поляризатор. Это было продемонстрировано на кристалле CdMgTe. Измерения светового потока кристалла использовались для расчета его постоянной Верде, которая характеризует силу эффекта Фарадея материала.
Вращение Фарадея
Вращение состояния поляризации из-за эффекта Фарадея называется вращением Фарадея, которое прямо пропорционально как напряженности магнитного поля (
Когда постоянная Верде известна, можно вычислить вращение Фарадея (

Один из подходов к получению постоянной Верде – измерение Фарадеевского вращения для определенной длины материала и известной напряженности магнитного поля.
Измерение эффекта Фарадея
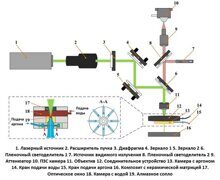
Используя данный подход и установку, показанную на рисунке 1, была измерена сила эффекта Фарадея в кристалле CdMgTe.

Рисунок 1. Измерения эффекта Фарадея могут быть выполнены с образцом, помещенным между источником линейно поляризованного света и поляризационно-чувствительной системой детектирования. Кристалл CdMgTe составлял приблизительно треть длины отверстия кольцевого магнита, а пластиковый держатель образца использовался для позиционирования и фиксации кристалла в центре отверстия. В системе детектирования датчик оптической мощности располагался как можно ближе к выходной стороне линейного поляризатора, который был установлен в держателе с индексированным вращением. Преимущество этой установки в том, что она требует минимального выравнивания.
Источник линейно поляризованного света состоял из коллимированного волоконного лазера 785 нм, излучение которого проходило через фиксированный линейный поляризатор.
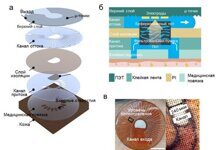
Для создания магнитного поля использовался кольцевой супермагнит, достаточно сильный, чтобы вызвать измеримое Фарадеевское вращение. Кристалл был установлен в центре отверстия магнита, так как именно там магнитное поле наиболее сильное (рис. 2).

Рисунок 2. Исследуемый кристалл помещался в отверстие кольцевого магнита (слева). Кристалл длиной 2,2 мм был расположен в центре отверстия длиной 6,35 мм, где магнитное поле было наиболее сильным, наиболее однородным и направлено вдоль оси N-S (справа).
Свет из кристалла выходил во второй линейный поляризатор, который был закреплен в держателе с индексированным вращением, и на датчик мощности. Датчик мощности располагался как можно ближе к выходной стороне линейного поляризатора.
Было получено два набора измерений, один с магнитом, а другой без магнита в установке. В каждом наборе данных (рисунок 3) регистрировалось изменение средней мощности при различных углах вращения второго поляризатора с шагом 2°. Кривые колеблются с одинаковым периодом, но сдвинуты по фазе (

Рисунок 3. Измерения оптической мощности производились при вращении второго поляризатора с шагом 2°. Данные были получены с магнитом вне (треугольники) и (квадраты) установки. Закон Малюса (сплошные линии) использовался при моделировании для соответствия каждой кривой. Сдвиг фазы (
Расчет постоянной Верде
Фазовый сдвиг между двумя кривыми на рисунке 3 связан с Фарадеевским вращением. Как описано в отдельной статье, чтобы получить Фарадеевское вращение, обычно необходимо добавить коэффициент к фазовому сдвигу. В этом случае этот коэффициент равен нулю, а фазовый сдвиг равен Фарадеевскому вращению.
Фазовый сдвиг может быть определен после аппроксимации каждой кривой по закону Малюса:

где

Таблица 1. Результаты эксперимента
|
Аппроксимация без магнита |
Аппроксимация с магнитом |
Вращение фарадея ( |
|
|
|
|
Напряженность магнитного поля (
© Thorlabs
Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по поставке лабораторного и научного оборудования производства Thorlabs на территории РФ
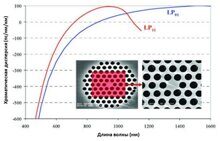
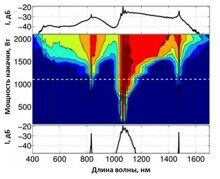
В статье описан метод генерации суперконтинуума, расширенного в видимый диапазон. За счет четырехволнового смешения накачка 1064 нм создает антистоксовы и стоксовы компоненты на 831 нм и 1478 нм. Фазовый синхронизм обеспечивается благодаря микроструктурированному мультимодальному волокну особой конструкции.
контакты
г. Санкт-Петербург, улица Савушкина 83, корп. 3