Микроскопия с применением иммерсионных объективов Mitutoyo
Перспективной технологией является микроскопия с использованием твердой иммерсионной линзы, приспособлением для повышения апертуры микроскопа, изготовленное из материала с высоким коэффициентом преломления.
Впервые было введено для преодоления дифракционного предела воздушно-связанных объективов в оптических микроскопах. Благодаря высокому показателю преломления в среде между объективом и образцом, значительно увеличивается числовая апертура (NA), тем самым улучшая разрешение системы визуализации.
Такие линзы привлекли гораздо больше внимания в области оптического хранения данных, позволив существенно улучшить емкости памяти. Они также нашли применение в ближнепольной сканирующей микроскопии из-за высокой эффективности на оси изображения. Однако для работы в широком поле зрения иммерсионные линзы вводят аберрации в систему, что ухудшает качество изображения.
Исследование иммерсионных объективов проводилось с использованием высококачественных объективов Mitutoyo, крупнейшего производителя микрообъективов. Микрообъективы имеют непревзойденные параметры яркости и выпускаются в нескольких сериях.
Серия FS предназначена для работы в светлом, темном поле, пропускают УФ и световое излучение, ИК волны. В планапохроматических объективах скорректированы аберрации для четырех и более длин волн. Гарантируется превосходная цветопередача и яркость изображения.
Серия ML - это объективы с высокой степенью коррекции аберраций. Корректировка даёт неоспоримые преимущества: можно изменять расстояние между тубусом и объективом, добавлять модули для ортоскопии, коноскопии, дополнительные светоделители. Большое рабочее расстояние позволяет получать резкие изображения объекта в широких пределах.
Сравнительные характеристики твердотельных иммерсионных линз
На рис. 1 показаны две конфигурации широко используемых твердотельных линз: а) полусферическая твердотельная иммерсионная линза (НSIL) и б) апланатическая твердотельная иммерсионная линза (ASIL). У первой линзы лучи из центра основания будут попадать на сферическую поверхность нормально и выходить без преломления. Длина волны внутри нее уменьшается в n раз, а показатель преломления, соответственно, увеличивает числовую апертуру объектива в n раз.
Рисунок 1. Конфигурации (а) полусферической и (б) апланатической SIL
Апланатическая иммерсионная линза на Рис. 1(б) представляет собой усеченную сферу толщиной, равной:

где r – радиус линзы. Лучи из центра основания будут преломляться на сферической поверхности, и расходящийся луч образует виртуальное изображение на расстоянии r × (1 + n) от вершины. По сравнению с первой линзой на поверхности сферы наблюдается некоторый изгиб луча, и числовая апертура в пространстве объекта увеличивается в n2 раз, а не в n.
В обеих конфигурациях точки расположения источника и изображения (Q и Q’) удовлетворяют апланатическому условию, когда нет никакой дополнительной сферической аберрации в оптической системе. Однако, если линзы используются в системе визуализации широкого поля, аберрации неизбежно возникнут для смещенных от центра точек объекта, и это может быть легко продемонстрировано точечными диаграммами на рис. 2.
Рисунок 2. Внеосевые точечные диаграммы изображения источника в полусферической линзе (А) и апаланатической (Б). В обоих случаях диск Эйри имеет радиус 1.3 мкм. Измерения получены для поля, радиус которого составляет 0.1 мм. Числовая апертура объектива 0.3
На рисунке 2 представлены точечные, полученные с помощью программы трассировки лучей. Средний элемент в каждой матрице - точечная диаграмма наилучшего изображения конкретной точки поля. Другие элемиенты матрицы - точечные диаграммы в плоскостях, расположенных в осевом направлении через равные промежутки времени от плоскости наилучшего изображения. Значение и знак под каждым квадратом - расстояние и направление от наилучшей плоскости изображения, а сплошной круг представляет собой воздушный диск в пространстве изображений.
Даже на самых гладких плоскостях точечные диаграммы показывают значительный разброс, указывающий на наличие аберраций; (2) наилучшими плоскостями изображения являются плоскости, на 3 и 13 мкм отстоящие от плоскостей изображения для двух линз. Эти плоскости показывают настоящую кривизну поля.
Моделирование
Аберрации вводятся в систему, если точка объекта смещена от центра и если толщина линзы имеет отклонения (±∆H), от H0 [указанного в уравнении (1)]. В этой статье используется компьютерная модель для изучения характеристик изображения, полученного с использованием апланатической иммерсионной линзы при различных ∆x и ∆H; также исследуется влияние радиуса ASIL на качество изображения.
Компьютерная модель
На рис.3 предполагается, что линза имеет толщину H0 ± ∆H. Точечный объект помещается в точку s на расстояние ∆x от оптической оси. Точечный объект испускает световой конус, перпендикулярный основанию линзы. Рассмотрим луч, который разворачивает угол Ө к оптической оси, при достижении сферической поверхности он преломляется и пересекает воображаемый экран q1 в точке g. При моделировании мы не учитываем эффекты поляризации, так как эти эффекты не являются значимыми из-за малости углов. Затем луч обратно распространяется по прямой линии ко второму воображаемому экрану q2. Таким образом, при взгляде справа луч будет казаться исходящим из точки М.
Рисунок 3. Cхема, используемая в компьютерной модели
Следуя тем же рассуждениям, все лучи внутри конуса света в точке s распространяются до экрана q2. Если точка q2 экрана совпала бы с параксиальной плоскостью изображения, то все лучи пересекли бы экран в точке m, если бы не было аберраций. Однако в целом это не так. Распределение изображения точки объекта получается путем суперпозиции всех плоских волн с учетом длин оптических путей лучей и мест их пересечения q2. Чтобы получить наилучшее положение изображения для этой конкретной исходной точки, осевое положение экрана q2 изменяется до тех пор, пока пик распределения изображения не достигнет максимума.
Функция распределения точек интенсивности и точечная диаграмма
На компьютере смоделированы четыре случая расположения апланатической иммерсионной линзы и точечного объекта, расположенного на оси и вне ее, а апланатические линзы с идеальной и неидеальной толщиной, результаты представлены на рис. 4. Для каждого случая в отдельности показана функция рассеяния точки (ФРТ) по лучшей плоскости изображения диаграммы точки и два профиля линии. Последние извлекаются из ФСР вдоль направления x и y, причем оба проходят через вершину ФСР. ∆x = 0, ∆H = 0 (первая строка на рис. 4): случай идеальной твердотельной линзы и точки объекта, расположенной на оси. Как и ожидалось, распределение имеет круговую симметрию, а FWHM составляет 1,09 мкм, что согласуется со значением, рассчитанным с использованием скалярной теории дифракции.
Рисунок 4. Результаты моделирования (слева направо): ФСР, точечная диаграмма и линейные профили ФСР в направлениях x (сплошная кривая) и y (пунктирная кривая)
∆x = 0, ∆H = 10 мкм (второй ряд на рис. 4): случай, когда объект находится на оси, но линза на 10 мкм толще номинального значения. Как и ожидалось, ФСР по-прежнему симметрична, но ее ширина намного больше, чем в первом случае. Действительно, на уровне FWHM ФСР увеличилась на 30%. Точечная диаграмма также увеличена, что означает, что она больше не является идеальным геометрическим изображением. Боковые лепестки ФСР также увеличились в размерах. Все это говорит о наличии в системе сферической аберрации.
∆x = 132 мкм (в компьютерной модели используется нормализованная единица измерения, которая равна 16NAimg, 132 мкм соответствует 1000 нормализованным единицам), ∆h = 0 (третья строка на рис. 4): случай, когда твердотельная линза идеальна, но объект смещен от центра на 132 мкм. Эта ширина поля (264 мкм) соответствует приблизительно 700 точкам разрешения на плоскости объекта в одном измерении. ФСР теперь деформирована и больше не симметрична в направлении x, вдоль которого была смещена точка объекта. Два линейных профиля не идентичны, и FWHM из них примерно на 10% шире, чем в первом случае.
Приведенное выше моделирование показывает, что апланатическая иммерсионная линза свободна от аберраций только тогда, когда ∆x = 0 и ∆H = 0. Если эти условия не выполняются, введенные аберрации ухудшают ФСР, тем самым влияя на разрешение системы. Из этих двух параметров ∆H, по-видимому, оказывает гораздо большее влияние на систему, чем ∆x. Отсутствие комы и астигматизма является показателем относительно хорошей внеосевой визуализации системы. Поле, содержащее 700 точек разрешения, достаточно для многих применений, но контроль толщины оптического компонента с точностью до нескольких микрометров потребует большей точности.
Кривизна поля
На рис. 2 показано, что кривизна поля является основной аберрацией, влияющей на качество изображения в апланатической твердотельной иммерсионной линзе.
Зависимость между размером поля и расстоянием расфокусировки была рассчитана с помощью компьютерного моделирования при различных толщинах линзы и представлена на Рис. 5.
На величину искривления поля также влияет толщина линзы. При ∆H = -10 мкм и +10 мкм наилучшие плоскости изображения находятся на расстояниях 10 и 16 мкм соответственно, измеренных при радиусе поля x = 100 мкм. Эти цифры говорят о том, что тонкая линза способствует появлению кривизны поля в меньшей степени, чем толсая, но в любом случае эти значения намного больше глубины фокуса линзы. Поэтому методы компенсации кривизны поля необходимы, если требуется изображение хорошего качества на большом поле.
Рисунок 5. Зависимость между радиусом поля (горизонтальным) и расстоянием расфокусировки с помощью компьютерной модели при различной толщине апланатической линзы
Влияние радиуса апланатической линзы на кривизну поля
Теоретически, на осевые изображения диаметр линзы не влияет до тех пор, пока толщина равна идеальному значению H0. Диаметр, однако, влияет на качество изображения вне оси, поскольку внеосевые аберрации тесно связаны с радиусом оптических элементов. Кривизна поля, например, будет меняться вместе с диаметром линзы. При фиксированном радиусе поля ∆x = 100 мкм расстояния расфокусировки в зависимости от радиуса линзы для трех толщин были рассчитаны с помощью программы трассировки лучей и показаны на рис. 6. Вертикальная ось задает расстояние расфокусировки относительно точки изображения на оси. Видно, что расстояние расфокусировки обратно пропорционально диаметру линзы. Это означает, что для снижения кривизны поля, следует использовать линзу с большим радиусом,.
Рисунок 6. Cмоделированный результат трассировки лучей, диаметр ASIL (горизонтальный) против расфокусировки (вертикальный) при радиусе поля 10 мкм с толщиной ASIL, равной H0 (сплошная кривая), на 5 мкм меньше (пунктирно–пунктирная кривая) и на 5 мкм больше (пунктирная кривая)
Из результатов, показанных на рис. 5 и 6, можно сделать вывод, что для относительно качественного широкополосного изображения лучше использовать линзу с большим диаметром.
Результаты экспериментов
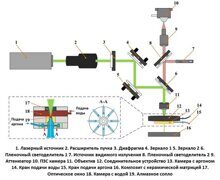
В статье рассмотрена система визуализации поля зрения с использованием апланатической твердотельной иммерсионной линзы, и установка показана на рис. 7. Система состоит из объектива Mitutoyo, в котором компенсированы хроматические и волновые аберрации. Рабочее расстояние объектива 20 мм. Ширина поля 1.2 мм.
Показатель преломления линзы принят n633 = 1,8449. Радиус 2,5 мм. Выбор радиуса линзы обусловлен доступными в лаборатории образцами. Пучок от HeNe-лазера попадает на вращающийся диффузор, создавая движущийся спекл-узор для освещения образца. Луч расширяется до заполнения всей апертуры объектива, чтобы полностью использовать числовую апертуру.
Рисунок 7. Экспериментальная установка, состоящая из объектива Mitutoyo 0.42 NA и линзы с радиусом 2.5 мм, n = 1.845 (пунктирный квадрат)
На практике существуют и другие факторы, ограничивающие эффективное функционирование системы. В нашей экспериментальной установке это механический держатель для линзы ASIL, который частично блокирует свет, проходящий через элемент.
Улучшение разрешения
Был проведен ряд экспериментов, демонстрирующих улучшение разрешающей способности и аберрационных характеристик системы. На рис. 8 показаны два изображения, полученные с использованием (а) только объектива Mitutoyo и (б) объектива с иммерсионной линзой. Объект представляет собой решетку с периодом, равным 1 мкм. Согласно критериям Рэлея, разрешение составляет 0,92 мкм для объектива с 0,42NA при длине волны 0,6328 мкм. Объект с периодом 1 мкм разрешим, поскольку взаимодействие ПЗС-матрицы, вместе с быстро движущейся спекл-картиной гарантирует снижение спекл-шума до достаточно низкого уровня и не влияет на качество изображения.
Рисунок 8. Изображения решетки с периодом 1 мкм. Длина волны освещения составляет 0,6328 мкм. На рис (а) - только объективом 0,42 NA Mitutoyo и (б) объективом Mitutoyo с линзой, радиусом r = 2,5, n = 1,845. Размер изображения 25 мкм
В следующем опыте сравнивается использование объектива, оснащенного апланатической линзой, и двух коммерческих объективов для микроскопов производства Zeiss и Olympus. Используемый образец представляет собой прямоугольную решетку с периодом, равным 2 мкм. Полученные изображения показаны на рис. 9., справа показаны профили интенсивности, извлеченные из изображений.
Рисунок 9. Широкопольные изображения от трех объективов (слева) и нормированные интенсивности (справа). Сверху вниз: объектив Zeiss, ASIL объектив и объектив Olympus соответственно. Объект представляет собой решетку с периодом 2 мкм
В правой колонке показаны профили интенсивности, извлеченные из изображений. Хорошо видно, что изображение с самым высоким разрешением получается с помощью объектива Zeiss, в то время как объектив Olympus дает изображение с наименьшим разрешением.
Кривизна поля
Моделирование на рис. 5 показывает величину кривизны поля, возникающей в результате использования апланатической иммерсионной линзы. Используемый объектив Mitutoyo имеет плоское поле выше 1,6 мкм при диаметре поля 1,2 мм. Это значение значительно меньше, чем кривизна поля, введенная линзой, и поэтому будет оказывать минимальное влияние на измерение.
Образец, используемый для измерения, представляет собой ту же решетку, что и на рис. 9.
Изображения решетки были сделаны с помощью камеры, расположенной в точках сетки, а затем изображения были обработаны для определения величины кривизны поля. Чтобы облегчить обработку сигнала, мы определили индекс фокусировки Ibf. Из каждого изображения извлекается строка данных (всегда одна и та же строка) и к ней применяется преобразование Фурье. Ibf задается отношением амплитуд третьей и первой гармоник, в результате чего получается в общей сложности 30 соотношений. Затем они нормализуются по отношению к той, которая имеет наибольшее отношение. Эти соотношения нанесены на рис.10 (а) в виде контуров. Горизонтальные координаты представляют положение поля (горизонтальное) и вертикальные - расстояние расфокусировки в микронах.
Рисунок 10. (а) Экспериментальное и (б) моделируемое отношение пространственных частот (третья гармоника к основной частоте)
На 10 (а) и 10 (б) видно, что исследуемая линза немного отклоняется от идеальной толщины. Наилучшие места фокусировки вдоль оптической оси для различных точек поля выделены из рис. 10 и нанесены на рис. 11 (пунктирная кривая).
Рисунок 11. Экспериментальные результаты (пунктирная кривая) описывают зависимость между размером поля (по горизонтали) и расстоянием расфокусировки (по вертикали). Остальные кривые – это компьютерные симуляции из рис. 5
Заключение
Изображение в иммерсионной твердотельной линзе исследовано как с использованием компьютерного моделирования, так и экспериментально. Установлено, что среди внеосевых аберраций кривизна поля является основной, влияющей на качество изображения апланатической твердотельной иммерсионной линзы. Смоделированы величины кривизны поля при различных толщинах линзы. Результаты показывают, что менее изогнутая плоскость изображения и, следовательно, относительно однородное качество изображения можно ожидать, если использовать ASIL с толщиной немного меньшей, чем идеальная, хотя это немного снизит резкость осевых изображений. Моделирование также показывает, что больший диаметр ASIL приводит к меньшей кривизне поля и, таким образом, дает изображения лучшего качества.
Высококачественные изображения оптических решеток получены с помощью микрообъективов производства Mitutoyo, числовая апертура которых была увеличена в 2 раза. Отмечено, что спроектированная система визуализации подойдет для проведения поверхностной плазмонно резонансной томографии. Из этих экспериментальных результатов мы видим, что микрообъективы в сочетании с линзой обеспечивает очень хорошее качество изображения в пределах достаточно большого поля.
© Applied Opt. Vol. 46, No. 20, 2007
Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Mitutoyo на территории РФ
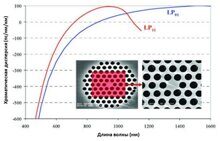
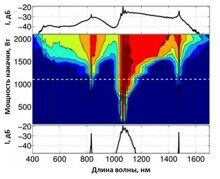
В статье описан метод генерации суперконтинуума, расширенного в видимый диапазон. За счет четырехволнового смешения накачка 1064 нм создает антистоксовы и стоксовы компоненты на 831 нм и 1478 нм. Фазовый синхронизм обеспечивается благодаря микроструктурированному мультимодальному волокну особой конструкции.
контакты
г. Санкт-Петербург, улица Савушкина 83, корп. 3